Generic Code
PSyclone is designed to be configurable so that new front-ends (called
APIs) can be built, re-using as much existing code as possible. The
generic code is kept in the psyGen.py file for psy-code generation.
New APIs
TBD
Existing APIs
LFRic (Dynamo0.3)
Mesh
The LFRic API supports meshes that are unstructured in the horizontal and structured in the vertical. This is often thought of as a horizontal 2D unstructured mesh which is extruded into the vertical. The LFRic infrastructure represents this mesh as a list of 2D cells with a scalar value capturing the number of levels in the vertical “column”.
Cells
In the LFRic API, kernels which have metadata which specifies
operates_on = CELL_COLUMN work internally on a column of
cells. This means that PSyclone need only be concerned with iterating
over cell-columns in the horizontal. (Kernels which have operates_on
= DOMAIN work internally on all available columns of cells and
therefore this iteration is not required.) As a result, the LFRic
infrastructure presents the mesh information to PSyclone as if the
mesh were 2-dimensional. From now on this 2D view will be assumed
i.e. a cell will actually be a column of cells. The LFRic
infrastructure provides a global 2D cell index from 1 to the number of
cells.
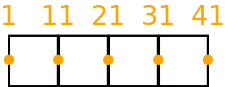
For example, a simple quadrilateral element mesh with 4 cells might be indexed in the following way.
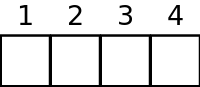
When the distributed memory option is switched on in the Dynamo0.3 API (see the Distributed Memory Section) the cells in the model are partitioned amongst processors and halo cells are added at the boundaries to a depth determined by the LFRic infrastructure. In this case the LFRic infrastructure maintains the global cell index and adds a unique local cell index from 1 to the number of cells in each partition, including any halo cells.
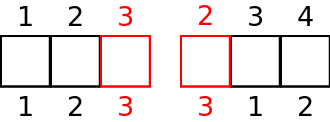
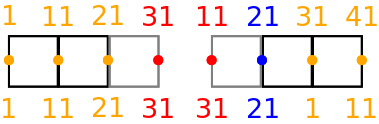
An example for a depth-1 halo implementation with the earlier mesh split into 2 partitions is given below, with the halo cells being coloured red. An example local indexing scheme is also provided below the cells. Notice the local indexing scheme is set up such that owned cells have lower indices than halo cells.
Dofs
In the LFRic infrastructure the degrees-of-freedom (dofs) are indexed from 1 to the total number of dofs. The infrastructure also indexes dofs so that the values in a column are contiguous and their values increase in the vertical. Thus, given the dof indices for the “bottom” cell, the rest of the dof indices can be determined for the column. This set of dof indices for the bottom cell is called a dofmap.
Dofs represent a field’s values at various locations in the mesh. Fields can either be continuous or discontinuous. Continuous fields are so named because their values are continuous across cell boundaries. Dofs that represent continuous fields are shared between neighbouring cells. Discontinuous fields have values that are not necessarily related between neighbouring cells (there can be discontinuities across cell boundaries). Dofs that represent discontinuous fields are local to a cell.
Discontinuous Dofs
A simple example of discontinuous dofs is given below. In this case each cell contains 1 dof and there are 10 cells in a column. We only show the bottom cells and their corresponding dof indices. As explained earlier, the dof indices increase contiguously up the column, so the cell above the cell containing dof index 1 contains dof index 2 and the cell above that contains dof index 3 etc.
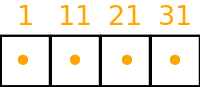
As discussed in the previous section, when the distributed memory option is switched on in the Dynamo0.3 API (see the Distributed Memory Section) the cells in the model are partitioned amongst processors and halo cells are added at the boundaries to a depth determined by the LFRic infrastructure. This results in the dofs being replicated in the halo cells, leading to a dof halo. As for cells, the LFRic infrastructure maintains the global dof indexing scheme and adds a local dof indexing scheme from 1 to the number of dofs in each partition, including any halo dofs.
An example for a depth-1 halo implementation with the earlier mesh split into 2 partitions is given below, with the halo cells drawn in grey and halo dofs coloured red. An example local partition indexing scheme is also provided below the dofs. As with cells, notice the local indexing scheme ensures that owned dofs have lower indices than halo dofs.
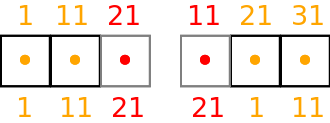
Continuous Dofs
A simple continuous dof example is given below for the same mesh as before. In this case dofs are on cell edges in the horizontal and there are 10 cells in a column. Again we only show the bottom cells and their corresponding dof indices. As explained earlier, the dof indices increase contiguously up the column, so the cell above the cell containing dof index 1 contains dof index 2 and the cell above that contains dof index 3 etc.
As already explained, when the distributed memory option is switched on in the Dynamo0.3 API (see the Distributed Memory Section) the cells in the model are partitioned amongst processors and halo cells are added at the boundaries.
In the example below we ignore the additional halo cells and just look
at the partitioning of cells amongst processors (with the same mesh
and 2 partitions as shown earlier). It can be seen that the dofs
shared between cells which are on different partitions now need to be
replicated if fields on continuous dofs are going to be able to be
computed locally on each partition. This concept is different to halos
as there are no halo cells here, the fact that the cells are
partitioned has meant that continuous dofs on the edge of the
partition are replicated. The convention used in Dynamo0.3 is that the
cell with the lowest global id determines which partition owns a
dof and which has the copy. Dofs which are copies are called
annexed. Annexed dofs are coloured blue in the example:

If we now extend the above example to include the halo cells (coloured grey) then we get:
An example for a depth-1 halo implementation with the earlier mesh split into 2 partitions is given below, with the halo cells drawn in grey and halo dofs coloured red. An example local indexing scheme is also provided below the dofs. Notice the local indexing scheme ensures that owned dofs have lower indices than annexed dofs, which in turn have lower indices than halo dofs.
Cell and Dof Ordering
Cells in a partition are sequentially indexed by the LFRic infrastructure, starting at 1, so that local cells occur first, then level-1 halo cells, then level-2 halo cells etc. A benefit of this layout is that it makes it easy for PSyclone to specify the required iteration space for cells as a single range, allowing a single Fortran do loop (or other language construct as required) to be generated. The LFRic infrastructure provides an API that returns the index of the last owned cell, the index of the last halo cell at a particular depth and the index of the last halo cell, to support PSyclone code generation.
Dofs on a partition are also sequentially indexed by the LFRic infrastructure, starting at 1, so that local dofs occur first, then annexed dofs (if the field is continuous), then level-1 halo dofs, then level-2 halo dofs etc. Again, this layout makes it easy for PSyclone to specify the required iteration space for dofs as a single range. As before, the LFRic infrastructure provides an API that returns the index of the last owned dof, the index of the last annexed dof, the index of the last halo dof at a particular depth and the index of the last halo dof, to support PSyclone code generation.
Multi-grid
The Dynamo 0.3 API supports kernels that map fields between meshes of
different horizontal resolutions; these are termed “inter-grid”
kernels. As indicated in Fig. 1 below, the change in
resolution between each level is always a factor of two in both the
x and y dimensions.
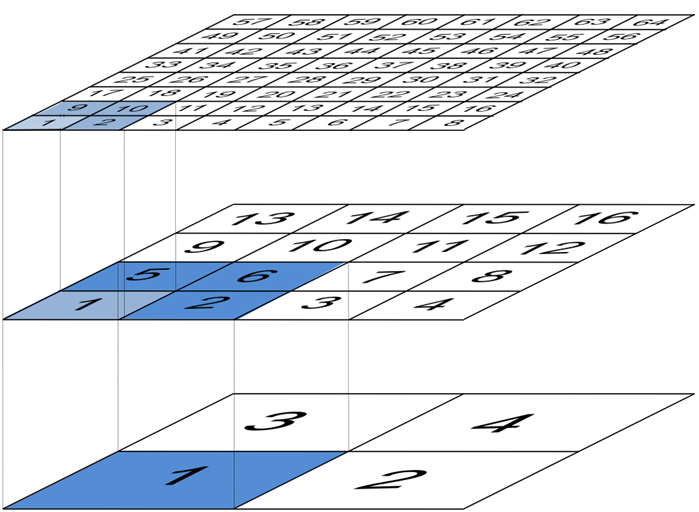
Fig. 1 The arrangement of cells in the multi-grid hierarchy used by LFRic. (Courtesy of R. Wong, Met Office.)
Inter-grid kernels are only permitted to deal with fields on two, neighbouring levels of the mesh hierarchy. In the context of a single inter-grid kernel we term the coarser of these meshes the “coarse” mesh and the other the “fine” mesh.
There are two types of inter-grid operation; the first is “prolongation” where a field on a coarse mesh is mapped onto a fine mesh. The second is “restriction” where a field on a fine mesh is mapped onto a coarse mesh. Given the factor of two difference in resolution between the fine and coarse meshes, the depth of any halo accesses for the field on the fine mesh must automatically be double that of those on the coarse mesh.
Loop iterators
In the current implementation of the Dynamo0.3 API it is possible to iterate (loop) either over cells or dofs. At the moment all coded kernels are written to iterate over cells and all Built-in kernels are written to iterate over dofs, but that does not have to be the case.
The loop iteration information is specified in the kernel metadata. In
the case of Built-ins there is kernel metadata but it is part of
PSyclone and is specified in
src/psyclone/parse/lfric_builtins_mod.f90.
For inter-grid kernels, it is the coarse mesh that provides the iteration space. (The kernel is passed a list of the cells in the fine mesh that are associated with the current coarse cell.)
Cell iterators: Continuous
Note that if PSyclone does not know whether a modified field is
discontinuous or continuous (because e.g. its function space is given
as ANY_SPACE_* in kernel metadata) then it must assume it is continuous.
When a kernel is written to iterate over cells and modify a continuous
field, PSyclone always (with the exception of GH_WRITE access -
see below) computes dofs on owned cells and redundantly
computes dofs in the level-1 halo (or to depth 2 if the field is on
the fine mesh of an inter-grid kernel - see Multi-grid). Users
can apply a redundant computation transformation to increase the halo
depth for additional redundant computation but it must always at least
compute the level-1 halo. The reason for this is to ensure that the
shared dofs on cells on the edge of the partition (both owned and
annexed) are always correctly computed. Note that the outermost halo
dofs are not correctly computed and therefore the outermost halo of
the modified field is dirty after redundant computation. Since shared
dofs for a field with GH_WRITE access are guaranteed to have the
same, correct value written to them, independent of whether or not
the current cell “owns” them, there is no need to perform redundant
computation in this case.
An alternative solution could have been adopted in Dynamo0.3 whereby no redundant computation is performed and partial-sum results are shared between processors in a communication pattern similar to halo exchanges. However, a decision was made to always perform redundant computation.
A downside of performing redundant computation in the level-1 halo is that any fields being read by the kernel must have their level-1 halo clean (up-to-date), which can result in halo exchanges.
This is also the case for a modified field with GH_READINC access
as readinc captures a kernel field whose data is read (into the
level-1 halo) and then incremented. However, the level-1 halo does not
need to be clean for a modified field with GH_INC access, as an
increment does not require the halo to be clean.
Whilst the level-1 halo does not need to be clean for a field with a
GH_INC access, the data in the level-1 halo will be read and
written. The data in the level-1 halo must therefore not cause any
exceptions, which can be the case with some compilers where the values
in the halo have not yet been written to (i.e. there will be an access
to uninitialised data).
To avoid this problem the user guide currently recommends that all
setval_c and setval_x Built-in calls (see
Built-ins for more details) compute to the level-1
halo (by using the redundant computation transformation). This will
guarantee that all modified halo data has been initialised with a
value. If redundant computation transformations have been added then
it is the outermost modified halo that will not require a halo
exchange i.e. a loop iterating to the level-n halo will result in
a halo exchange to the level-(n-1) halo being added before the
loop, so the above Built-in calls would need to compute redundantly to
the appropriate depth. In the future it may be that we should require
fields with halos to have all of their data initialised to a set value
when they are created, add an option to PSyclone, default to computing
redundantly for the above Built-ins, or generate code that sets the
halo to a specific value locally before the loop is called.
Cell iterators: Discontinuous
When a kernel is written to iterate over cells and modify a discontinuous field, PSyclone only needs to compute dofs on owned cells. Users can apply a redundant computation transformation (see the Transformations section) to redundantly compute into the halo but this is not done by default.
Dof iterators
When a kernel that is written to iterate over dofs modifies a field,
PSyclone must ensure that all dofs in that field are updated. If the
distributed memory flag is set to false then PSyclone must iterate
over all dofs. PSyclone simply needs to create a loop that iterates
from 1 to the total number of dofs. The latter value is provided by
the LFRic API.
If the distributed memory flag is set to true then PSyclone must
ensure that each partition only iterates over owned dofs. Again PSyclone
just needs to create a loop that iterates from 1 to the total number
of owned dofs on that partition. The latter value is provided by the
LFRic API.
When the distributed memory flag is set to true an aditional
configuration option can be set which makes PSyclone always create
loops which iterate over both owned and annexed dofs. Whilst this is
not necessary for correctness, it can improve performance by reducing
the number of halo exchanges required (at the expense of computing
annexed dofs redundantly). The only change for PSyclone is that it
calls a different LFRic routine which returns the index of the last
annexed dof. This iteration space will necessarily also include all
owned dofs due to the ordering of dof indices discussed earlier.
The configuration variable is called COMPUTE_ANNEXED_DOFS and is
found in the dynamo0.3 section of the psyclone.cfg
configuration file (see Configuration). If it is true then
annexed dofs are always computed in loops that iterate over dofs and
if it is false then annexed dofs are not computed. The default in
PSyclone is false.
The computation of annexed dofs could have been added as a transformation optimisation. The reason for using a configuration switch is that it is then guaranteed that annexed dofs are always computed for loops that iterate over dofs which then allows us to always remove certain halo exchanges without needing to add any new ones.
If we first take the situation where annexed dofs are not computed for
loops that iterate over dofs i.e. (COMPUTE_ANNEXED_DOFS is false),
then a field’s annexed dofs will be dirty (out-of-date) after the loop
has completed. If a following kernel needs to read the field’s
annexed dofs, then PSyclone will need to add a halo exchange to make
them clean.
There are five cases to consider:
the field is read in a loop that iterates over dofs,
the field is read in a loop that iterates over owned cells and level-1 halo cells,
the field is incremented in a loop that iterates over owned cells and level-1 halo cells,
the field is read in a loop that iterates over owned cells, and
the field is written in a loop that iterates over owned cells.
In case 1) the annexed dofs will not be read as the loop only iterates
over owned dofs so a halo exchange is not required. In case 2) the
full level-1 halo will be read (including annexed dofs) so a halo
exchange is required. In case 3) the annexed dofs will be updated so a
halo exchange is required. In case 4) the annexed dofs will be read so
a halo exchange will be required. In case 5) the annexed dofs will be
written with correct values (a condition of a kernel with GH_WRITE
for a continuous field) so no halo exchange is required.
If we now take the case where annexed dofs are computed for loops that
iterate over dofs (COMPUTE_ANNEXED_DOFS is true) then a field’s
annexed dofs will be clean after the loop has completed. If a
following kernel needs to read the field’s annexed dofs, then
PSyclone will no longer need a halo exchange.
We can now guarantee that annexed dofs will always be clean after a continuous field has been modified by a kernel. This is because loops that iterate over either dofs or cells now compute annexed dofs and there are no other ways for a continuous field to be updated.
We now consider the same four cases. In case 1) the annexed dofs will now be read, but annexed dofs are guaranteed to be clean, so no halo exchange is required. In case 2) the full level-1 halo is read so a halo exchange is still required. Note, as part of this halo exchange we will update annexed dofs that are already clean. In case 3) the annexed dofs will be updated but a halo exchange is not required as the annexed dofs are guaranteed to be clean. In case 4) the annexed dofs will be read but a halo exchange is not required as the annexed dofs are guaranteed to be clean.
Furthermore, in the 3rd and 4th cases (in which annexed dofs are read
or updated but the rest of the halo does not have to be clean), where
the previous writer is unknown (as it comes from a different invoke
call) we need to add a speculative halo exchange (one that makes use of
the runtime clean and dirty flags) when COMPUTE_ANNEXED_DOFS is
False, as the previous writer may have iterated over dofs, leaving
the annexed dofs dirty. In contrast, when COMPUTE_ANNEXED_DOFS is
True, we do not require a speculative halo exchange as we know that
annexed dofs are always clean.
Therefore no additional halo exchanges are required when
COMPUTE_ANNEXED_DOFS is changed from false to true i.e. case 1)
does not require a halo exchange in either situation and case 2)
requires a halo exchange in both situations. We also remove halo
exchanges for cases 3) and 4) so the number of halo exchanges may be
reduced.
If a switch were not used and it were possible to use a transformation to selectively perform computation over annexed dofs for loops that iterate over dofs, then we would no longer be able to guarantee that annexed dofs would always be clean. In this situation, if the dofs were known to be dirty then PSyclone would need to add a halo exchange and if it were unknown whether the dofs were dirty or not, then a halo exchange would need to be added that uses the run-time flags to determine whether a halo exchange is required. As run-time flags are based on whether the halo is dirty or not (not annexed dofs) then a halo exchange would be performed if the halo were dirty, even if the annexed dofs were clean, potentially resulting in more halo exchanges than are necessary.
Halo Exchange Logic
Halo exchanges are required when the DISTRIBUTED_MEMORY flag is set to
true in order to make sure any accesses to a field’s halo or to its
annexed dofs receive the correct value.
Operators and Halo Exchanges
Halo Exchanges are only created for fields. This causes an issue for
operators. If a loop iterates over halos to a given depth and the loop
includes a kernel that reads from an operator then the operator must
have valid values in the halos to that depth. In the current
implementation of PSyclone all loops which write to, or update an
operator are computed redundantly in the halo up to depth-1 (see the
load() method in the LFRicLoop class). This implementation therefore
requires a check that any loop which includes a kernel that reads from
an operator is limited to iterating in the halo up to
depth-1. PSyclone will raise an exception if an optimisation attempts
to increase the iteration space beyond this (see the gen_code()
method in the LFRicKern class).
To alleviate the above restriction one could add a configurable depth with which to compute operators e.g. operators are always computed up to depth-2, or perhaps up to the maximum halo depth. An alternative would be to halo exchange operators as required in the same way that halo exchanges are used for fields.
First Creation
When first run, PSyclone creates a separate InvokeSchedule for each of the
invokes found in the algorithm layer. This schedule includes all required
loops and kernel calls that need to be generated in the PSy layer for
the particular invoke call. Once the loops and kernel calls have been
created then (if the DISTRIBUTED_MEMORY flag is set to true) PSyclone
adds any required halo exchanges and global sums. This work is all
performed in the LFRicInvoke constructor (__init__) method.
In PSyclone we apply a lazy halo exchange approach (as opposed to an eager one), adding a halo exchange just before it is required.
It is simple to determine where halo exchanges should be added for the initial schedule. There are four cases:
loops that iterate over cells and modify a continuous field will access the level-1 halo. This means that any field that is read within such a loop must have its level-1 halo clean (up-to-date) and therefore requires a halo exchange. A modified field (specified as
GH_INCwhich involves a read before a write) will require a halo exchange if its annexed dofs are not clean, or if their status is unknown. Whilst it is only the annexed dofs that need to be made clean in this case, the only way to acheive this is via a halo exchange (which updates the halo i.e. more than is required). Note, if theCOMPUTE_ANNEXED_DOFSconfiguration variable is set totruethen no halo exchange is required as annexed dofs will always be clean.loops that iterate over cells and modify a continuous field but specify GH_WRITE access are a special case since the value to be written to any dof location is guaranteed to be independent of loop iteration (i.e. the current cell column). As such, annexed dofs are not required to be clean since they are not accessed.
continuous fields that are read from within loops that iterate over cells and modify a discontinuous field will access their annexed dofs. If the annexed dofs are known to be dirty (because the previous modification of the field is known to be from within a loop over dofs) or their status is unknown (because the previous modification to the field is outside of the current invoke) then a halo exchange will be required (As already mentioned, currently the only way to make annexed dofs clean is to perform a halo swap. Note, if the
COMPUTE_ANNEXED_DOFSconfiguration variable is set totruethen no halo exchange is required as annexed dofs will always be clean.fields that have a stencil access will access the halo and need halo exchange calls added.
Halo exchanges are created separately (for fields with halo reads) for
each loop by calling the create_halo_exchanges() method within the
LFRicLoop class.
In the situation where a field’s halo is read in more than one kernel in different loops, we do not want to add too many halo exchanges - one will be enough as long as it is placed correctly. To avoid this problem we add halo exchange calls for loops in the order in which they occur in the schedule. A halo exchange will be added before the first loop for a field but the same field in the second loop will find that there is a dependence on the previously inserted halo exchange so no additional halo exchange will be added.
The algorithm for adding the necessary halo exchanges is as follows:
For each loop in the schedule, the create_halo_exchanges() method
iterates over each field that reads from its halo (determined by the
unique_fields_with_halo_reads() method in the LFRicLoop class).
For each field we then look for its previous dependencies (the previous writer(s) to that field) using PSyclone’s dependence analysis. Three cases can occur: 1) there is no dependence, 2) there are multiple dependencies and 3) there is one dependence.
If no previous dependence is found then we add a halo exchange call before the loop (using the internal helper method
_add_halo_exchange()). If the field is a vector field then a halo exchange is added for each component. The internal helper method_add_halo_exchangeitself uses the internal helper method_add_halo_exchange_code(). This method creates an instance of theLFRicHaloExchangeclass for the field in question and adds it to the schedule before the loop. You might notice that this method then checks that the halo exchange is actually required and removes it again if not. In our current situation the halo exchange will always be needed so this check is not required but in more complex situations after transformations have been applied to the schedule this may not be the case. We discuss this type of situation later.If multiple previous dependencies are found then the field must be a vector field as this is the only case where this can occur. We then choose the closest one and treat it as a single previous dependency (see 3).
If a single previous dependency is found and it is a halo exchange then we do nothing, as it is already covered. This will only happen when more than one reader depends on a writer, as discussed earlier. If the dependence is not a halo exchange then we add one.
After completing the above we have all the halo exchanges required for correct execution.
Note that we do not need to worry about halo depth or whether a halo is definitely required, or whether it might be required, as this is determined by the halo exchange itself at code generation time. The reason for deferring this information is that it can change as transformations are applied.
Halo Exchanges and Loop transformations
When a transformation (such as redundant computation) is applied to a loop containing a kernel, it can affect the surrounding halo exchanges. Consider the following example:
0: Loop[type='dofs', upper_bound='nannexed']
0: BuiltIn setval_x(f2,f1)
1: HaloExchange[field='f1', check_dirty=True]
2: Loop[type='cells', upper_bound='cell_halo(1)']
0: CodedKern testkern_code(f2,f1)
A potential halo exchange for field f1 is required as the
testkern_code kernel reads field f1 in its level 1 halo.
If we transform the code so that the setval_c kernel computes
redundantly to the level 1 halo:
0: HaloExchange[field='f1', check_dirty=True]
1: Loop[type='dofs', upper_bound='dof_halo(1)']
0: BuiltIn setval_x(f2,f1)
2: Loop[type='cells', upper_bound='cell_halo(1)']
0: CodedKern testkern_code(f2,f1)
then a potential halo exchange for field f1 is now required before
the setval_c kernel and the halo exchange before the
testkern_code kernel is not required (as it is covered by the
first halo exchange).
After such a transformation is applied then halo exchanges are managed by checking whether 1) any fields in the modified kernel now require a halo exchange before the kernel and adding them if so and 2) any existing halo exchanges after the loop, that were added due to fields being modified in the loop, are still required and removing them if not. Performing these 2 steps maintains halo exchange correctness and continues to minimise the number of required halo exchanges.
Note, the actual halo exchange extents (their depths) are computed dynamically so are not a concern at this point.
A general rule is that a halo exchange must not have a dependence with another halo exchange, as this would mean that one of them is not required. PSyclone should raise an exception if it finds this situation.
However, due to the two step halo exchange management process, there can be a transient situation after the first step where a halo exchange can temporarily depend on another halo exchange. If we revisit the previous example and consider the state of the system once the first step (checking whether halo exchanges are required before the modified kernel) has completed:
0: HaloExchange[field='f1', check_dirty=True]
1: Loop[type='dofs', upper_bound='dof_halo(1)']
0: BuiltIn setval_x(f2,f1)
2: HaloExchange[field='f1', check_dirty=True]
3: Loop[type='cells', upper_bound='cell_halo(1)']
0: CodedKern testkern_code(f2,f1)
we have a transient situation where a halo exchange has been added
before the setval_x kernel but the halo exchange before the
testkern_code kernel has not yet been removed. Therefore, when
adding, updating or removing halo exchanges the test for whether halo
exchanges have a dependence between each other must be temporarily
disabled. This is achieved by the ignore_hex_dep argument being
set to True in the _add_halo_exchange_code function within the
LFRicLoop class and the actual check that is skipped is implemented
in the _compute_halo_read_info function within the
LFRicHaloExchange class.
Asynchronous Halo Exchanges
The Dynamo0p3AsynchronousHaloExchange transformation allows the default synchronous halo exchange to be split into a halo exchange start and a halo exhange end which are represented separately as nodes in the schedule. These can then be moved in the schedule to allow overlapping of communication and computation, as long as data dependencies are honoured.
A halo exchange both reads and modifies a field so has a readwrite
access for dependence analysis purposes. An asynchronous halo exchange
start reads the field and an asynchronous halo exchange end writes to
the field. Therefore the obvious thing to do would be to have the
associated field set to read and write access respectively. However,
the way the halo exchange logic works means that it is simplest to set
the halo exchange end access to readwrite. The reason for this is that
the logic to determine whether a halo exchange is required
(_required()) needs information from all fields that read from the
halo after the halo exchange has been called (and therefore must be
treated as a write with following reads for dependence analysis) and
it needs information from all fields that write to the field before
the halo exchange has been called (and therefore must be treated as a
read with previous writes for dependence analysis). An alternative
would be to make the _required() method use the halo exchange start
for previous writes and the halo exchange end for following
reads. However, it was decided that this would be more complicated
than the solution chosen.
Both halo exchange start and halo exchange end inherit from halo
exchange. However, the halo exchange start and end are really two
parts of the same thing and need to have consistent properties
including after transformations have been performed. This is achieved by
having the halo exchange start find and use the methods from the halo
exchange end, rather than implement them independently. The actual
methods needed are _compute_stencil_type(),
_compute_halo_depth() and _required(). It is unclear how much
halo exhange start really benefits from inheriting from halo exchange
and this could probably be removed at the expense of returning
appropriate names for the dag, colourmap, declaration etc.
Note
The dependence analysis for halo exchanges for field vectors is currently over zealous. It does not allow halo exchanges for independent vector components to be moved past one another. For example, a halo exchange for vector component 2, if placed after a halo exchange for component 1 could not be moved before the halo exchange for component 1, even though the accesses are independent of each other. This is also the case for asynchronous halo exchanges. See issue #220.
Evaluators
Evaluators consist of basis and/or differential basis functions for a
given function space, evaluated at the nodes of another, ‘target’,
function space. A kernel can request evaluators on multiple target
spaces through the use of the gh_evaluator_targets metadata entry.
Every evaluator used by that kernel will then be provided on all of the
target spaces.
When constructing a LFRicKernMetadata object from the parsed kernel
metadata, the list of target function-space names (as they appear in
the meta-data) is stored in LFRicKernMetadata._eval_targets. This
information is then used in the LFRicKern._setup() method which
populates LFRicKern._eval_targets. This is an OrderedDict which has
the (mangled) names of the target function spaces as keys and 2-tuples
consisting of FunctionSpace and DynKernelArgument objects as
values. The DynKernelArgument object provides the kernel argument
from which to extract the function space and the FunctionSpace object
holds full information on the target function space.
The DynInvokeBasisFunctions class is responsible for managing the
evaluators required by all of the kernels called from an Invoke.
DynInvokeBasisFunctions._eval_targets collects all of the unique target
function spaces from the LFRicKern._eval_targets of each kernel.
DynInvokeBasisFunctions._basis_fns is a list holding information on
each basis/differential basis function required by a kernel within the
invoke. Each entry in this list is a dict with keys:
Key |
Entry |
Type |
|---|---|---|
shape |
Shape of the evaluator |
str |
type |
Whether basis or differential basis |
str |
fspace |
Function space |
FunctionSpace |
arg |
Associated kernel argument |
DynKernelArgument |
qr_var |
Quadrature argument name |
str |
nodal_fspaces |
Target function spaces |
list of (FunctionSpace, DynKernelArgument) |
Precision
The different types (kinds) of precision for scalar, fields and
operators are specified in the lfric_constants.py file. Adding a
new precision (kind) name to PSyclone for the LFRic (Dynamo0.3) API
should simply be a case of adding the appropriate entry to this
file. Doing this will provide a working version, but, of course, it
ignores any additional tests, an example and updating the
documentation. The suggested approach here would be to search for an
existing precision type e.g. r_tran and see where and how this is
used in tests and examples and where it is mentioned in the
documentation.
Modifying the Schedule
Transformations modify the schedule. At the moment only one of these
transformations - the Dynamo0p3RedundantComputationTrans class in
transformations.py - affects halo exchanges. This transformation can
mean there is a requirement for new halo exchanges, it can mean
existing halo exchanges are no longer required and it can mean that
the properties of a halo exchange (e.g. depth) can change.
The redundant computation transformation is applied to a loop in a
schedule. When this is done the update_halo_exchanges() method for
that loop is called - see the apply() method in
Dynamo0p3RedundantComputationTrans.
The first thing that the update_halo_exchanges() method does is call
the create_halo_exchanges() method to add in any new halo exchanges
that are required before this loop, due to any fields that now have a
read access to their halo when they previously did not. For example, a
loop containing a kernel that writes to a certain field might
previously have iterated up to the number of owned cells in a
partition (ncells) but now iterates up to halo depth 1.
However, a field that has its halo read no longer guarantees that a
halo exchange is required, as the previous dependence may now compute
redundantly to halo depth 2, for example. The solution employed in
create_halo_exchanges() is to add a halo exchange speculatively and
then remove it if it is not required. The halo exchange itself
determines whether it is required or not via the required() method. The
removal code is found at the end of the _add_halo_exchange_code()
method in the LFRicLoop() class.
The second thing that the update_halo_exchanges() method does is check
that any halo exchanges after this loop are still required. It finds
all relevant halo exchanges, asks them if they are required and if
they are not it removes them.
We only need to consider adding halo exchanges before the loop and removing halo exchanges after the loop. This is because redundant computation can only increase the depth of halo to which a loop computes so can not remove existing halo exchanges before a loop (as an increase in depth will only increase the depth of an existing halo exchange before the loop) or add existing halo exchanges after a loop (as an increase in depth will only make it more likely that a halo exchange is no longer required after the loop).
Kernel Transformations
Since PSyclone is invoked separately for each Algorithm file in an application, the naming of the new, transformed kernels is done with reference to the kernel output directory. All transformed kernels (and the modules that contain them) are re-named following the PSyclone Fortran naming conventions (Fortran Naming Conventions). This enables the reliable identification of transformed versions of any given kernel within the output directory.
If the “multiple” kernel-renaming scheme is in use, PSyclone simply appends an integer to the original kernel name, checks whether such a kernel is present in the output directory and if not, creates it. If a kernel with the generated name is present then the integer is incremented and the process repeated. If the “single” kernel-renaming scheme is in use, the same procedure is followed but if a matching kernel is already present in the output directory then the new kernel is not written (and we check that the contents of the existing kernel are the same as the one we would create).
If an application is being built in parallel then it is possible that
different invocations of PSyclone will happen simultaneously and
therefore we must take care to avoid race conditions when querying the
filesystem. For this reason we use os.open:
fd = os.open(<filename>, os.O_CREAT | os.O_WRONLY | os.O_EXCL)
The os.O_CREATE and os.O_EXCL flags in combination mean that
open() raises an error if the file in question already exists.
Colouring
If a loop contains one or more kernels that write to a field on a continuous function space then it cannot be safely executed in parallel on a shared-memory device. This is because fields on a continuous function space share dofs between neighbouring cells. One solution to this is to ‘colour’ the cells in a mesh so that all cells of a given colour may be safely updated in parallel (Fig. 2).
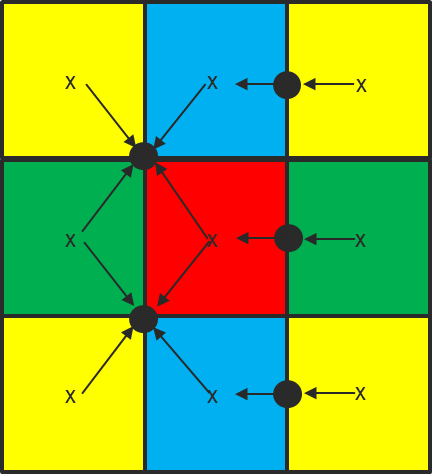
Fig. 2 Example of the colouring of the horizontal cells used to ensure the thread-safe update of shared dofs (black circles). (Courtesy of S. Mullerworth, Met Office.)
The loop over colours must then be performed sequentially but the loop
over cells of a given colour may be done in parallel. A loop that
requires colouring may be transformed using the Dynamo0p3ColourTrans
transformation.
Each mesh in the multi-grid hierarchy is coloured separately (https://code.metoffice.gov.uk/trac/lfric/wiki/LFRicInfrastructure/MeshColouring) and therefore we cannot assume any relationship between the colour maps of meshes of differing resolution.
However, the iteration space for inter-grid kernels (that map a field from one mesh to another) is always determined by the coarser of the two meshes. Consequently, it is always the colouring of this mesh that must be used. Due to the set-up of the mesh hierarchy (see Fig. 1), this guarantees that there will not be any race conditions when updating shared quantities on either the fine or coarse mesh.
Lowering
As described in Back-ends for the PSy-layer, the use of a PSyIR backend to
generate code for the LFRic PSy layer requires that each LFRic-specific
node be lowered to ‘language-level’ PSyIR. Although this is work in progress
(see e.g. https://github.com/stfc/PSyclone/issues/1010), some nodes already
have the lower_to_language_level() method implemented. These are
described in the sub-sections below.
BuiltIns
In the LFRic PSyIR, calls to BuiltIn kernels are represented by a
single Node which is a subclass of LFRicBuiltIn.
The lower_to_language_level() methods of these BuiltIn nodes must
therefore replace that single Node with the
PSyIR for the arithmetic operations required by the particular BuiltIn.
This PSyIR forms the new body of the dof loop containing the original
BuiltIn node.
In constructing this PSyIR, suitable Symbols for the loop
variable and the various kernel arguments must be looked up. Since the
migration to the use of language-level PSyIR for the LFRic PSy layer
is at an early stage, in practise this often requires that suitable
Symbols be constructed and inserted into the symbol table of the PSy
layer routine. A lot of this work is currently performed in the
DynKernelArgument.infer_datatype() method but ultimately (see
https://github.com/stfc/PSyclone/issues/1258) much of this will be
removed.
The sum and inner product BuiltIns require extending PSyIR to handle
reductions in the GlobalSum class in psyGen.py. Conversions from
real to int and vice-versa require the target precisions be
available as symbols, which is being implemented as a part of the mixed
precision support.
Kernel Metadata
LFRic captures its kernel metadata in a set of classes. These classes allow access to the metadata in a simple, structured way. They also allow the metadata to be modified, new metadata to be created and metadata to be loaded from its Fortran representation as well as being written back out to its Fortran representation.
Classes
The class to capture overall metadata is LFRicKernelMetadata. This class makes use of separate classes for each of the metadata declarations, such as MetaArgsMetadata and MetaFuncsMetadata. If necessary, the declaration classes make use of further classes which specify the individual metadata entries, such as ScalarArgMetadata and MetaFuncsArgMetadata. Where possible, common functionality is captured in a hierarchy of subclasses.
At the moment the metadata classes used in the GOcean API are distinct from the ones used in the LFRic API. Any common functionality between the two will be shared using common classes in the future.
Reading and Writing
Each class can load metadata from its Fortran representation via a Fortran string. This allows parts of the metadata to be loaded at a time or all of the metadata to be loaded in one go. Each class can also write out its metadata as a Fortran string. For example
fortran_string = "func_type(w0, gh_basis_function)"
funcs_arg = MetaFuncsArgMetadata.create_from_fortran_string(fortran_string)
fortran_string = funcs_arg.fortran_string()
fortran_string = (
"type(func_type) :: meta_funcs(1) = "
"(/func_type(w0, gh_basis_function)/)\n")
meta_funcs = MetaFuncsMetadata.create_from_fortran_string(fortran_string)
fortran_string = meta_funcs.fortran_string()
fortran_string = "..."
lfric_metadata = LFRicKernelMetadata.create_from_fortran_string(
fortran_string)
fortran_string = lfric_metadata.fortran_string()
Each class can also load metadata from an fparser2 tree representation. The examples below make use of a utility method to transform from a fortran string to a fparser2 tree. However, in practice loading from an fparser2 tree will only be used if the tree already exists.
fortran_string = "func_type(w0, gh_basis_function)"
fparser2_tree = MetaFuncsArgsMetadata.create_fparser2(
fortran_string, Fortran2003.Part_Ref)
funcs_arg = MetaFuncsArgMetadata.create_from_fparser2(fparser2_tree)
fortran_string = funcs_arg.fortran_string()
fortran_string = (
"type(func_type) :: meta_funcs(1) = "
"(/func_type(w0, gh_basis_function)/)\n")
fparser2_tree = MetaFuncsMetadata.create_fparser2(
fortran_string, Fortran2003.Data_Component_Def_Stmt)
meta_funcs = MetaFuncsMetadata.create_from_fparser2(fparser2_tree)
fortran_string = meta_funcs.fortran_string()
fortran_string = "..."
fparser2_tree = LFRicKernelMetadata.create_fparser2(
fortran_string, Fortran2003.Derived_Type_Def)
lfric_metadata = LFRicKernelMetadata.create_from_fparser2(fparser2_tree)
fortran_string = lfric_metadata.fortran_string()
Creating Metadata
The classes can be used to create metadata, rather than reading it from existing metadata. For example
field_arg = FieldArgMetadata("GH_REAL", "GH_READ", "W0")
meta_funcs_arg = MetaFuncsArgMetadata("W0", basis_function=True)
lfric_metadata = LFRicKernelMetadata(
operates_on="DOMAIN", meta_args=[field_arg],
meta_funcs=[meta_funcs_arg], procedure_name="KERN_CODE",
name="kern_type")
fortran_string = lfric_metadata.fortran_string()
Modifying Metadata
All of the metadata class values have setters which allow the metadata to be simply modified. For example
field_arg = FieldArgMetadata("GH_REAL", "GH_READ", "W0")
field_arg.datatype = "GH_INTEGER"
field_arg.function_space = "W3"
Validation
All input values are validated against the valid set of values that could be used in the particular context. For example, the access type for a field argument can be one of gh_read, gh_write, gh_readwrite, gh_inc and gh_readinc. Valid values are stored in the LFRicConstants class within psyclone.domain.lfric.lfric_constants. An invalid value will cause an exception that indicates the problem in a user friendly way.
At the moment there is no constraint checking between different metadata values. For example, if a meta_func entry is specified for the w0 function space then at least one of the the meta_arg arguments must be on the w0 function space. However, this is not checked in the current implementation.
GOcean1.0
TBD
NEMO
Usage
In general, the details of how PSyclone is used when building a
particular model (such as LFRic) are left to the build system of
that model. However, PSyclone support for the NEMO model is still
evolving very rapidly and is not yet a part of the official NEMO
repository. Consequently, the PSyclone repository contains two
example scripts that are used when building the NEMO model.
These scripts may be found in examples/nemo/scripts and their
use is described in the README.md file in that directory.
PSyIR Construction
Since NEMO is an existing code, the way it is handled in PSyclone is
slightly different from those APIs that mandate a PSyKAl separation of
concerns (LFRic and GOcean1.0). As with the other APIs, fparser2 is
used to parse the supplied Fortran source file and construct a parse
tree (in psyclone.generator.generate). This parse tree is then
passed to the NemoPSy constructor which uses the fparser2 PSyIR
frontend to construct the equivalent PSyIR. (This PSyIR is
‘language-level’ in that it does not contain any domain-specific
constructs.) Finally, the PSyIR is passed to the NemoInvokes
constructor which applies various ‘raising’ transformations which
raise the level of abstraction by introducing domain-specific
information.
Implicit Loops
When constructing the PSyIR of NEMO source code, PSyclone currently
only considers explicit loops as candidates for being
raised/transformed into NemoLoop instances. However, many of the
loops in NEMO are written using Fortran array notation. Such use of
array notation is encouraged in the NEMO Coding Conventions
[nem13] and identifying these loops can be important
when introducing, e.g. OpenMP. Currently these implicit loops are not
automatically ‘raised’ into NemoLoop instances but can be done
separately using the NemoAllArrayRange2LoopTrans transformation.
However, not all uses of Fortran array notation in NEMO imply a loop. For instance,
ascalar = afunc(twodarray1(:,:))
means that the function afunc is passed the (whole of the)
twodarray1 and returns a scalar value. (The requirement for
explicit array shapes in the NEMO Coding Convention means that any
quantity without such a shape must therefore be a scalar.)
Alternatively, a statement that assigns to an array must imply a loop:
twodarray2(:,:) = bfunc(twodarray1(:,:))
but it can only be converted into an explicit loop by PSyclone if the
function bfunc returns a scalar. Since PSyclone does not currently
attempt to fully resolve all symbols when parsing NEMO code, this
information is not available and therefore such statements are not
identified as loops (issue
https://github.com/stfc/PSyclone/issues/286). This may then mean that
opportunities for optimisation are missed.